Where are Negative Numbers in 3 dimensions?
The Covid Pandemic gave me time to study negative numbers. This reignited my frustration with the √-1 = i. The concept of i as a 90O rotation on a circle makes sense. Understanding why multiplying an i with an i results in -1 is more difficult.
I also wanted to make sense of i and negative numbers in 3 dimensions. To do this I needed to study movement in 3 dimensions. I found it difficult to imagine rotations and needed a physical prop to try them out. I went on-line to see if I could buy a 3d sphere that showed rotation but could not find one. I decided to make my own.
Making a Rotation Ball
During Covid, the Irish government decided not to allow me to use my tennis balls for tennis. Both golf and tennis were forbidden for very questionable reasons. I decided to make my own 3d sphere and I took a Wilson Triniti eco-friendly tennis ball from my dusty sports bag. The only writing on the ball was the Triniti logo which I used to represent the North Pole. I cut off some of the felt with the logo using a scissors.
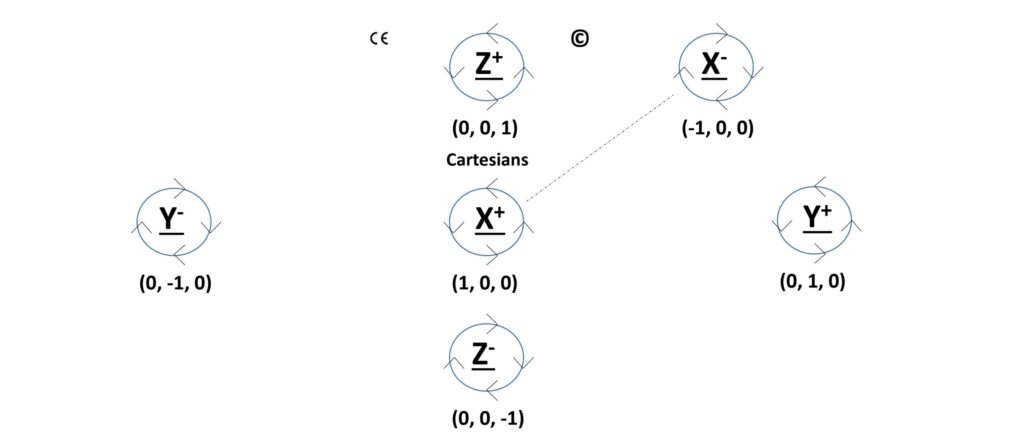
- At the North Pole, with the Triniti logo the right way around, I wrote Z+ in the centre of the logo to represent the positive end of the z-axis. I wrote the Cartesian coordinates (0, 0, 1) below the logo. See the diagram above.
- I marked Z- in the centre on the opposite side of the tennis ball and (0, 0, -1) below.
By holding the tennis ball at these Z+ and Z- points between my thumb and big finger, I had made the z-axis. I was able to rotate the tennis ball easily with my other hand.
- Holding the ball vertically by the z-axis, I then marked in the X+ pole in the centre facing me and (1, 0, 0) just below. I marked the X- pole in the centre on the opposite side with (-1, 0, 0) just below to get the x-axis.
- Continuing to hold the ball at the z-axis points, I turned it 90O counterclockwise or to the left and marked in the Y+ pole in the centre with (0, 1, 0) just below and then the Y- pole on the opposite side with (0, -1, 0) just below.
Counterclockwise and Clockwise Rotation
Turning counterclockwise and clockwise on the tennis ball can be confusing as the ball and your viewpoint seem to change. To make sure I was moving correctly I marked the counterclockwise rotation on the ball using the following diagram.
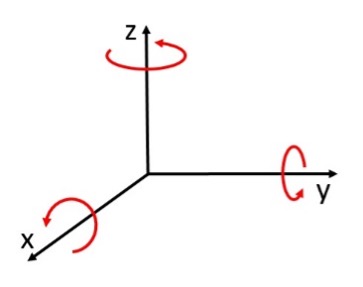
- With Z+ facing me and X+ below, I drew the symbol
around the Z+. This was to show the direction of the counterclockwise or positive rotation, no matter what angle I held the tennis ball. I turned the ball and then drew the symbol 
around the Z- to show clockwise rotation. - With Y+ facing me and Z+ facing me I drew the symbol around the Y+ and turning the ball drew around the Y-.
- With X+ facing me and Z+ above me I drew the symbol around the X+ and turning the ball drew around the X-.
To check that my arrows were correct, I held each axis parallel to the ground with the positive side towards me. Rotation clockwise and counterclockwise around the axis is then in the same direction as for a clock. i.e. The top of the ball moves left during a counterclockwise rotation and right during a clockwise rotation. I then realised that if I was looking at one side of the ball and it was moving left, the other side was moving right. You cannot really use left and right when describing rotation. If I want the ball to rotate counterclockwise, I need to check that it is moving in the direction of the arrows and vice versa for clockwise.
The Rotation Ball was ready but it needed a nickname. I decided to call it the R-Ball. The next blog describes how to use the R-Ball and continues the search for negative numbers.
